Abstract. Interoperability between two different blockchains, for instance to transfer funds, is often implemented using a bridge, a separate, newly created intermediary which interacts between the two blockchains. We show that, given that both blockchain have a zkRollup and therefore a zkVM, it is relatively straightforward to implement blockchain interoperability without the need for a separated trusted authority or additional trust assumptions. The cross-chain transaction thus obtained inherits the security properties of its underlying primitives.
We also show a different design called parallel rollups, and show how such systems can increase cross-chain operability and resolve liquidity fragmentation.
Keywords: Entangled Rollups, zkRollups, Interoperability, Blockchain, Smart Contract
Each blockchain is a essentially an island in the middle of the ocean, an isolated entity unaware of the outside world or the existence of other chains. However, many instances arise in which we would like blockchains to communicate to each other, to send arbitrary messages and, more specifically, to transfer assets.
The current solution adopted is called a bridge, a separate, intermediate entity, which is trusted with holding assets during some period of the transaction. This trust assumption is undesirable since it provides a potential point of failure: while your assets are in transfer, the bridge can be hacked (as has happened already many times [3]) or suddenly go out of service, leaving you with no re course.
The main result of our research can be stated as follows: Assuming the existence of a zkRollup on base chain B, it is possible to implement cross-chain asset transfer from A to B without the need for additional trust assumptions or trusted entities, just by combining the underlying primitives in a clever way.
The main goal of this paper is to make this intuition precise by detailing the underlying primitives and providing a step-by-step logical reasoning. The paper also outlines how an entangled rollup can be applied to improve liquidity optimization and implement a universal settlement layer.
Probably the most interesting proposal is zkBridge [11] developed by Polyhedra Network. The model in their is more rudimentary, starting from honest nodes that run a blockchain, whereas we already assume the existence (equivalence) of an L2 Rollup Ledger functionality. zkBridge uses zkSNARKs [7] specifically developed for each consensus mechanism, while we can use a zkVM, thus speeding up development time. There is also a difference in emphasis: we focus on asset transfer as the most imprtant use case leading us to discuss asset invariance for each transaction, while zkBridge merely treat asset transfer as a special kind of message.
Other projects developing zero knowledge (zk) bridging solutions in various stages include Succinct Labs, zkIBC by Electron Labs. These initiatives utilize zkSNARKs to enhance bridge designs. Central to their success is a light client protocol for efficient blockchain interaction and state synchronization.
Note that we claim our proposal uses the same security assumptions that already exist in a zkRollup. So we need to describe carefully how a Layer2 prepares a zk rollup and sends it to Layer1, and make implicit security assumptions explicit. Then, by combining these primitives, we obtain cross-chain asset transfer (i.e. the functionality that a bridge provides) without adding security assumptions (like an additional trusted party).
These consideration suggest the following structure for this paper: Section 2 reviews some notions such as zkVM and zk rollup. Section 3 focuses on correctness and defines asset invariance, which are applies in Section 4 which details L1-to-L2 and L2-to-L1 transactions in a zk rollup. Section 5 summarizes properties obtained and outlines the strategy to implement cross-chain transactions, which is presented in detail Section 6 applied to to two base chains. In Section 7 we show that by lifting our techiques to L2 some large advantages may be obtained, whereas Section 8 shows how more privacy can be obtained. Section 9 concludes with open problems and future research.
In verifiable computing, a computationally weak party outsources some computation \( F() \) with input \( x \) to a strong party. The latter not only computes the result \( y \), but also provides a validity proof in order to show that the result \( y = F(x) \) was computed correctly. Such a validity proof is often called a zero knowledge proof, even though this terminology is incorrect strictly speaking, since zero knowledge is a way to define privacy, a way of saying the a protocol not leaks any useful information[6] However, in many contexts, such as rollups, privacy isn't an issue, since the transactions are made public anyway. What is important, though, is the succinctness of such a proof, since on-chain verification is expensive and therefore should be efficient. Even though it is very unsatisfactory to use terminology that historically speaking is incorrect, we will adhere to the field's custom to use 'zk' to mean 'succinct', not 'private'.
Over the last decade we have seen tremendous progress in the practical realization of verifiable computing. Initially, a computation (program execution) was represented R1CS, and later by Boolean and arithmetic circuits, which are then transformed into polynomials. This process is called arithmetization. All these proofs are summarized under the term SNARK, standing for Succinct Non-interactive ARgument of Knowledge[8]. A problem of this approach is that for each program \( F() \) a new SNARK has to be developed, and creating a SNARK is prone to errors.
To side-step this problem, a new approach is to automate this process by using a zk virtual machine, or zkVM. The role of a zkVM is as follows. As input it accepts the execution trace of the computation \( y = F(x) \) performed on some specific processor architecture, such as MIPS, Risc5, WASM etc.
Since a computation happens in steps, its overall state can be defined by the values of a finite list of variables. A valid computation is a sequence of states, from a well-defined initial state to some final state, in which each state transition represents a valid computation step. This sequence can be represented as a table whose columns represent the list of variables and whose rows represent each step of the computation. This execution table is then converted in some huge, complicated polynomial which allows succinct verification of the statement "\( y = F(x) \)".
In a rollup, transaction processing is taken off-chain, combined into batches, in order to reduce cost and enhance speed. But the result of every transaction will be recorded on the base chain, as well as the overall rollup ledger’s state. However, there always a delay between the core L2 and it being recorded on L1.
In the words of Vitalik Buterin, whose concise blogpost [5] is an excellent introduction, rollups move computation (and state storage) off-chain, but keep some data per transaction on-chain. To improve efficiency, they use a whole host of fancy compression tricks to replace data with computation wherever possible. [...]
There is a smart contract on-chain which maintains a state root: the Merkle root of the state of the rollup (meaning, the account balances, contract code, etc, that are ”inside” the rollup). Anyone can publish a batch, a collection of transactions in a highly compressed form together with the previous state root and the new state root (the Merkle root after processing the transactions). The contract checks that the previous state root in the batch matches its current state root; if it does, it switches the state root to the new state root.
In other words, a Rollup emulates the ledger functionality on top of the original blockchain, which are called Layer 2 and Layer 1, respectively. In a rollup, the validity of L2 transactions is guaranteed by L1: each state transition is maintained, verified and endorsed by the base chain. L1 therefore needs an external verification mechanism, independent of the L2 implementation. For this purpose, two mechanisms are commonly used:
Fault proofs, as used by optimistic rollups In an optimistic rollup, some entity, usually called the Sequencer, publishes (oldStateRoot2, txBatch, newStateRoot2) on Layer1. This batch is accepted, until proven otherwise; hence the term optimistic. During some period of time (often seven days) this state change can be challenged by an outsider. If no such challenge takes place, the proposed state becomes permanent, but if a state change is challenged, then the following happens. There exists an arbitration contract on L1 which is activated by the Challenger, who deposits a bond. This contract will decide who is right: the Sequencer or the Challenger. As a result, the loser of this arbitration will be punished by having its stake or bond slashed. For a more detailed description about optimistic rollups, see for instance [9].
Validity proofs, as used in zk rollups In a validity proof, a different approach is taken. For every state transition \( \mathit{oldStateRoot}, \mathit{txBatch} \longrightarrow \mathit{newStateRoot2} \) a proof of knowledge is generated, which shows that \( \mathit{newStateRoot} \) is the correct result of executing the batch.
In a zkRollup, users submit a transaction to a node, which forwards it to a Sequencer, whose task it is to bundle many transactions into a batch, call the zkVM to compute a proof, and send it to L1.
Let \( STF \) denote the state transition function for the Layer 2 ledger. If the Sequencer is honest, we must have that \( \mathit{newState} = STF(\mathit{oldState}, \mathit{txBatch}) \). So by applying verifiable computing on \( STF \), L1, or rather, somebody who is monitoring this base chain, can be convinced that L2 indeed computed \( \mathit{newState} \) correctly from \( \mathit{oldState} \) and \( \mathit{txBatch} \). In particular, the execution trace of computing \( \mathit{newState} = STF(\mathit{oldState}, \mathit{txBatch}) \) is sent to a zkVM, which produces a succinct, non-interactive validity proof for this computation, which can be verified by the zkVerifier smart contract on L1.
The rollup contract on L1 has a method which, on input \( (\mathit{oldState}, \mathit{batch}, \mathit{newState}, \mathit{zkProof}) \), verifies the proof and returns an ACCEPT/REJECT verdict. In case of an ACCEPT, \( \mathit{oldState}, \mathit{batch}, \mathit{newState} \) are recorded as valid on L1, while in case of REJECT the batch and state change are simply discarded.
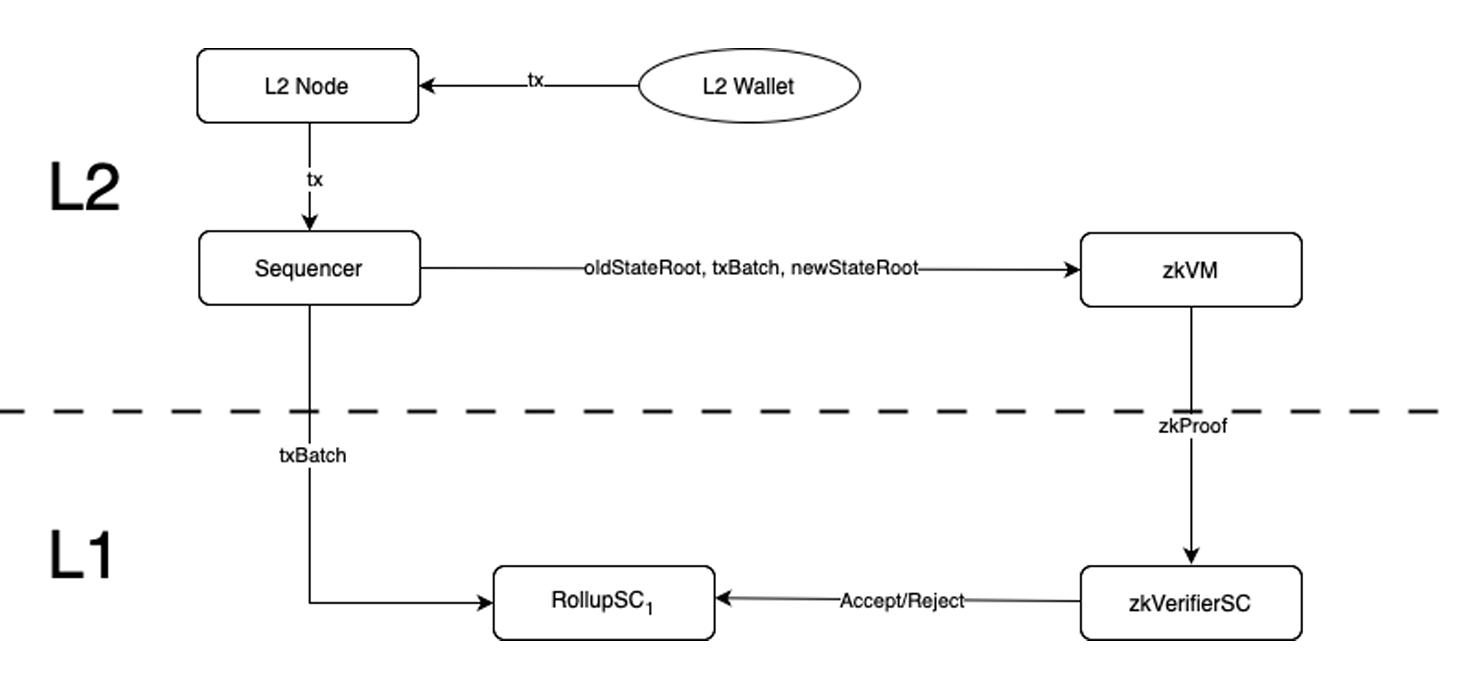
Sequencer
In this section we discuss what guarantees the correctness of a transaction on L1 and of a transaction on the rollup. An important aspect of correctness is asset invariance, which we define now. Let L represent Layer 1 or Layer 2. Blockchains are ledgers and therefore each transaction is only valid if it maintains the amount of assets invariant, expressed by the equation
\[ \mathit{totalAssets},\ (\mathit{newState},) = \mathit{totalAssetsL}(\mathit{oldState}) \]
For account-based L1s, asset invariance of a transaction can be verified by only summing the balance differences for those accounts \( i \) included in the transaction: \( \sum_i \mathit{newBalance}_i = \sum_i \mathit{oldBalance}_i. \) In UTXO-based L1s, the UTXO equation is exactly defined as to enforce this invariant, including returning change to the payer.[2] Note that minting, for instance for rewarding validation (mining) efforts, increases the amount of total assets in the new state, but to simplify the discussion we do not consider mining in the remainder of our paper.
\[ \mathit{RollupSCI}(\mathit{oldStateRoot}, \mathit{compressedTxBatch}, \mathit{newStateRoot}, \mathit{zkProof}) \]
Correctness of L1 transaction execution Correct execution of a transaction between two or more accounts on the same L1 is guaranteed since each L1 chain implements atomic transactions. This means that a transaction either succeeds or is aborted and rolled back, thus never leaving the blockchain in an inconsistent state. Its correctness implementation is guaranteed because the L1 software is open source; we therefore assume that many people have looked at it and eventual errors have been corrected.
Correctness of L2 transaction execution The situation for L2 and its rollup is more subtle. We assume the existence of an open source reference im plementation for L2 which is correct and preserves asset invariance. In practice, this reference implementation will often be a copy of L1, to maintain compatibility. However, a priori there is no reason to believe that batch proposers have followed this implementation faithfully. That’s why the rollup data is published on L1 and why a rollup must have a verification mechanism.
In the context of an optimistic rollup, a Challenger must show that that there is an error in the batch proposer if compared to this reference implementation. In the case of a zk rollup, the zkVM verifies that the rollup data published on L1 is consistent with the ledger program on L2.
A small but important detail is this: in a traditional protocol for proof-of knowledge [6] a human verifier only needs to make sure that his program V is correct. But a human verifying a zk rollup must also convince himself that the state transition function STF for L2 is correctly following the reference implementation. Again, the zk rollup verifies consistency of the rollup data published with the program submitted to the zkVM, but if this program contains an error, then the zkVerifier smart contract on L1 will not catch this.
In summary, the correctness of zk rollup transaction execution fundamentally depends on the correctness of the L2 reference implementation, correct implementation of the zkVM, correct invocation of the zkVM (with the right program to be verified), and correct implementation of the zkVerifier smart contract on L1. The issue of software correctness is of great concern, but out of the scope of this (theoretical) paper.
Given an L1 with an L2 rollup, asset transfers between the two layers occur naturally. Using Ethereum in the example, we have two direction:
Up, from L1 to L2: deposit (or buy) L2 assets: lock ETH on L1, and obtain ETH2 (the “wrapped” token created for L2);
Down, from L2 to L1: withdraw (or sell) L2 assets: lock ETH2 and redeem them as ETH on L1
To accomplish asset invariance, the rollup defines auxiliary asset transfer accounts on both layers, called RollupAccL (where L stands for Layer 1 or Layer 2) which are accessed through the smart contracts RollupSCL. The rollup accounts serve to lock and unlock assets in sync, which is the rollup’s way to maintain the sum of its assets on L1 and L2 constant.
To avoid discussion about lock/unlock vs. burn/mint, we assume that, on initialization, a huge fixed quantity of ETH2 is minted for (credited to) \( \mathit{RollupAcc}_2. \)
These assets must be kept locked in this L2 account, only to be unlocked by an equivalent lock transaction on L1. In this way asset invariance is preserved:
\[ \mathit{Balance}(\mathit{RollupAcc}_1) + \mathit{Balance}(\mathit{RollupAcc}_2) = \mathit{InitialQuantity}, \, \text{always}. \]
Upwards from L1 to L2 When transferring assets from L1 to L2, there are two alternatives. In the first alternative, RollupSC1simply performs the transaction both on L1 as well as on the rollup data. This implies extra work for the Sequencer who must ensure that the data on L2 is consistent with this state change. Note that many rollups have implemented this procedure as an emergency mechanism against censorship by Sequencers who refuse to include a user’s transaction. This alternative has some advantages: atomicity is guaranteed by L1, and transaction settlement time is short. But on the other hand, it makes sequencing harder, and results in higher gas cost.
In the second alternative, the smart contract on L1 produces a proof of transaction, sends it to the sequencer as a trigger for the transaction on L2. The smart contract on L2 trusts L1 blindly, so this proof-of-transaction can just be a simple L1 txid. Note that there are several ways L2 can receive the txid: Sequencer monitors L1; Sequencer is warned by smart contract L1; Sequencer is warned by Client X, etc.
In this alternative asset invariance is no longer guaranteed by atomicity. It uses another principle: first destroy (lock, burn) the asset; create a proof of this fact; then create (unlock, mint) the corresponding value elsewhere upon handing over the proof, which is then destroyed. This principle is sound because if, for some reason, the asset is not created, some party will have an economic loss and thus has an incentive to complain. Whereas if it were the other way around, some party might obtain assets for free and remain silent about it.
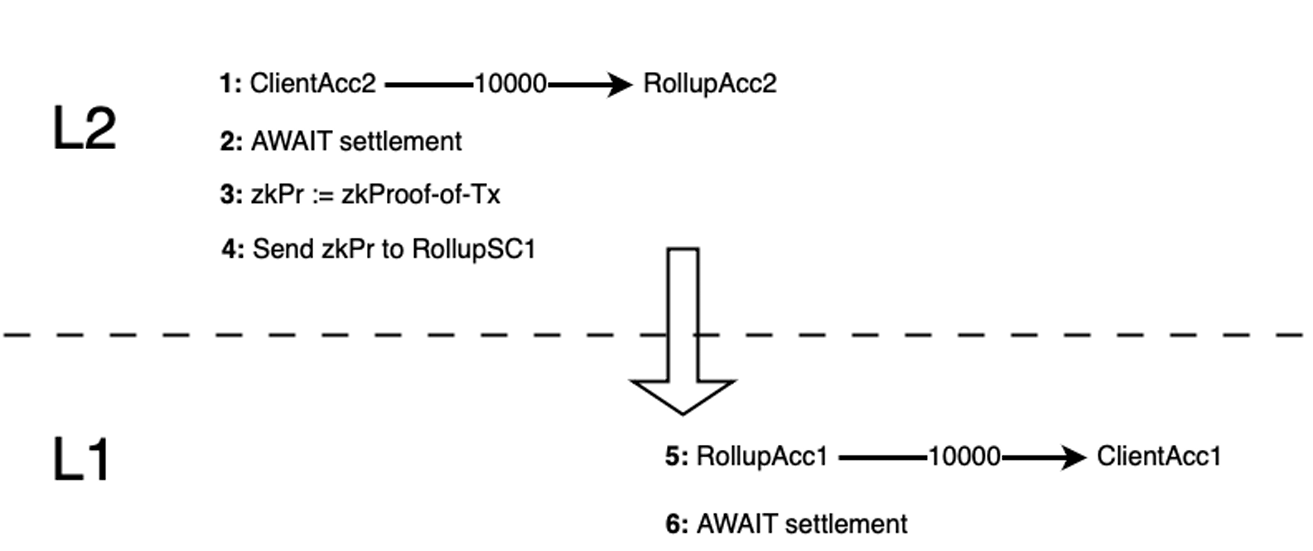
Downwards from L2 to L1 n this case, the Sequencer produces a proof of transaction, sends it to \(\mathit{RollupSC}_1\), which triggers the transaction on L1. However, since L1 does not trust L2 blindly, this proof-of-transaction has to be a zk proof. More specifically, it can provide a proof that the \(\mathit{ETH2}\) lock transaction is included in a transaction batch which has been finalized. Asset invariance is again guaranteed through the first-destroy-then-create principle.
We now describe the process step by step in a scenario in which user \(X\) wants to transfer \(z\) ETH from L2 to L1, in which subscripts denote the layer. This scenario is also depicted in Figure 4.
We now list assumptions and properties of a downward transaction in a zk rollup.
So in Protocol 1, the zk proof-of-transaction works like a certified cheque. It guarantees that assets have been destroyed (locked, burnt) on L2 so they can be redeemed on L1. Of course, measures should be taken to assure that a cheque can be cashed only once. Maintaining a list of previously cashed cheques is good solution (combined with expiration dates to avoid that the list grows forever).
In the context of a zk rollup, the statement proven is strictly related to the rollup. By applying verifiable computing on the state transition function, it is possible to prove that the Sequencer indeed computed newState2 correctly from oldState2 and txBatch, and this is confirmed on L1 by RollupSC1.
However, the fact that the Sequencer has access to a zkVM means that it is possible to prove more general statements about the state of the rollup data. For instance, it is possible to generate proofs for statements such as “Transaction tx has been finalized” (without involving the whole batch), or “At block height T user account X2 had 10000 ETH2 in its account”.
Observe that the statements in these examples are all relative to L2 and the rollup. But it is also possible to be even more general, and to generate a zk proof about some transaction on chain A and send it to chain B. This what we show in the next section.
Suppose we want to transfer assets from base chain A1 to B1. We just saw how zk proofs can be used as proof-of-transaction downwards from L2 to L1. We now want to apply this same idea by sending zk proofs-of-transaction horizontally, from A to B. The reverse direction can be obtained trivially by inverting the roles of A and B.
For concreteness let us consider Bitcoin and Ethereum. Since we have two different base chains, an atomic transaction is out of the question, so we resort to first-destroy-then-create. We can use Protocol 1, but substituting L2 for A1 (source) and L1 for B1 (destination). The proof of transaction will be a zk proof, which acts like a certified cheque showing that assets have been destroyed on A1.
How can one convince ETH that some asset destruction transaction tx on BTC indeed has taken place? Neither chain has a priori any reason to believe anything coming from the outside or from another chain; this is counter to the trust assumption of a blockchain. But both will accept a full-fledged zk proof that a transaction has been settled on the other chain.
There are two strategies to do this.
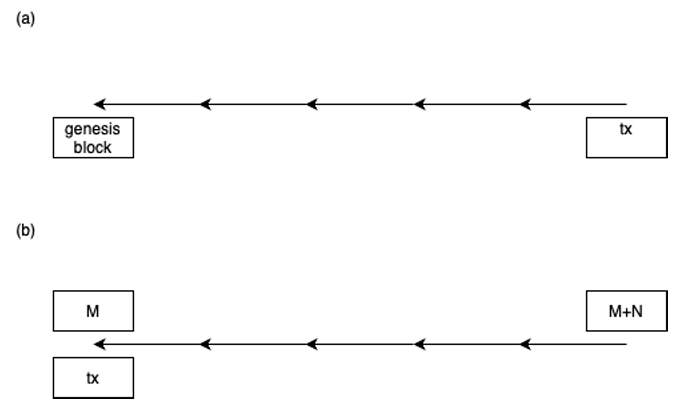
Backward zk proof-of-Transaction: Mina uses linear recursive proofs to seal all the information on its blockchain, an infinitely growing structure, down to a constant size [1]. This works because one knows the genesis block and one knows what constitutes a valid transaction, which can be captured and verified using zk proofs. And by using proof recursion one can guarantee that proof size does not increase. Mina started before zkVMs existed, so specific SNARKs have been developed to make this idea work. Today we can take advantage of a zkVM, which greatly simplifies this task.
Suppose a smart contract on ETH has the genesis block of BTC hard-coded in it. Then one can do the following: the transaction data is sent to a zkProver who, using recursive proof techniques, produces a zk proof of settlement. tx and zk proof get send to the smart contract on ETH, which verifies and accepts. Since this proves that some asset has been destroyed on A1, the creation of equivalent value on some other chain is authorized, thus ensuring asset invariance.
However, this does not prove that tx has been settled (that no rollback took place). For this reason, the next strategy is preferable.
Forward zk proof-of-Transaction Say \(\mathit{tx}\) is included in block \(M\). We wait \(N\) blocks, where \(N\) is sufficiently large to guarantee that no rollback has taken place. The hash of the block \(M+N\) is included in the zk proof-of-transaction. Suppose that \(\mathit{zkProver}\) understands the logic of BTC settlement, maybe by using a light client for payment verification. Therefore it can generate a proof that:
The reason why this constitutes a zk proof that tx has been settled is this: if somebody could falsify such a proof, this would be equivalent to developing an alternative fork for BTC, which, by assumption, is impossible. By using proof recursion techniques this proof can be succinct, a couple of hundred bytes.
We call the protocol obtained by moving Protocol 1 from the L2-L1 scenario to the A1-B1 scenario an entangled rollup since it entangles base chain A and B. The transfer accounts on A and B to maintain asset invariance in this context are called shadow accounts, while the two corresponding smart contracts are called shadow contracts. This leads to the following protocol.
The entangled rollup presented in Protocol 2 realizes cross-chain asset trans fer from A1 to B1 from a zk rollup, without introducing an intermediate entity or additional trust assumption. This can be verified by consulting the list of assumptions and properties inherited from protocol 1 (see 5.1. The only difference is Property 4, since now the zk proof statements are no longer restricted to transactions on the rollup, but related to settlement of transactions on the source chain A. So the entangled rollup inherits all the properties of the zk rollup, including those related to correctness.
For concreteness, the example above used a BTC-to-ETH transaction, but it is clear that transactions between other currencies is possible, provided that the following conditions are satisfied:
So, even though reversing the transaction from B1 to A1 in principle is not a problem, in the case of ETH to BTC it is, since the Script language of BTC is not sufficiently powerful to implement a zkVerifier. The BitVM project is an

effort to solve this problem by using a philosophy similar to optimistic rollups. See [10].
Using pairwise entangled rollups it will be possible to connect base chains such as BTC, ETH, AVE, etc˙allowing asset transfer using zk proofs as proof-of transaction. However, this vision has a problem, which we address in the section on liquidity optimization.
Yet another, promising generalization is this. Given a small number of blockchains, another interesting possibility is to implement a zk rollup in parallel on each un derlying blockchains. In other words, one L2 with a rollup, whose rollup data is maintained on several different L1s, as depicted in diagram XXX. In this case we assume that all transaction requests must first go to the Sequencer. Of course, all copies of the rollup data have to be identical.
For this parallel rollup, we can imagine a warped asset that’s pegged to the asset of some L1, or that a separate (meta)asset is created. Yet another possibility is that the rollup is extended to deal with multiple assets at the same time. After all, a rollup just implements the functionality of a ledger, and multiple currencies can be accommodated by adding an additional field specifying the type of currency. See Figure 6.
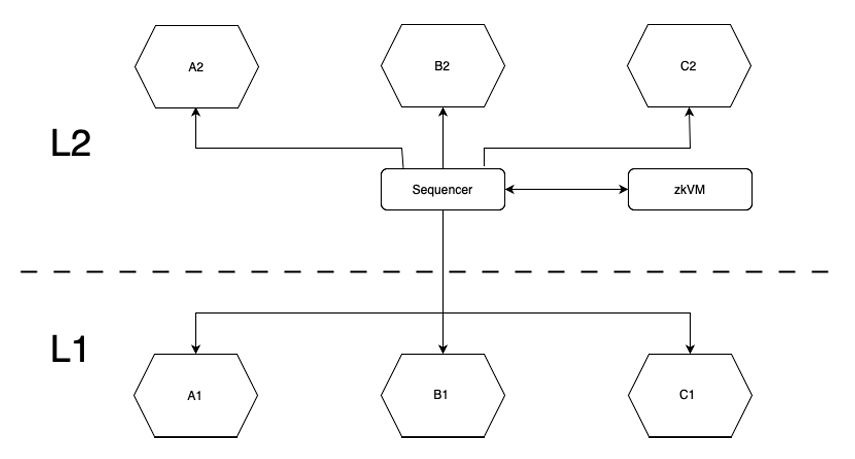
In the previous section we showed that asset transfer between two L1 blockchains is possible. However, there might be a liquidity problem. Suppose we have an asset, like USDT, and suppose that a client on A1 wants to transfer 10000 USDT to his account on B1. Then it is necessary that ShadowAccB, the shadow account on B1, has at least 10000 USDT in reserve, otherwise the transaction cannot be completed since there is not sufficient liquidity on B1. This situation is similar to exchanging cash currency on the airport: the exchange may not have the desired currency available for you to buy.
However, if we consider the same transaction between two L2s, things may be different. The shadow contract on A2 just needs to destroy 10000 USDT, while the shadow contract on B2 needs to create 10000 USDT. But since the currency on L2 is virtualized (pegged, wrapped), and assuming that one entity controls USDT on both A2 and B2, then this entity can simply perform this transaction without needing the real backing of USDT. Since both transactions take place on L2, asset destruction and creation is simply an accounting trick, it doesn’t have to be backed by real assets, so there is no liquidity problem.
This is, in essence, the idea of liquidity optimization. Imagine that a currency such as USDT appears on several L2s: USDT-ETH, USDT-AVE, USDT SOL, USDT-ALGO, ... Then by using entangled rollups it is straightforward to transfer from one L2 to another. So instead of having liquidity fragmentation, in which assets are stuck on some chain and transfers among them are restricted by asset reserves, now assets can flow easily from one L2 to another, offering unified access and higher liquidity. To make the point, having 1000 USDT deposited on Ethereum and 1000 USDT deposited on Avalanche turns into 2000 USDT of usable liquidity across all Layer 2s.
Observe that, for this to work, we must assume that the same entity controls the cryptocurrency on the two L2s. If this isn’t the case, liquidity optimization will not work. As a (counter)example, we are not claiming that one can simply transfer Arbitrum’s ARB into Optimism’s OP; without additional provisions this will be impossible.
Note that the data in zk proof, such as source address, destination address, amount, etc. is revealing and can be subject to chain analysis. If we want to obtain privacy, these fields can be concealed using encryption or hash function. For instance, suppose that the zk proof-of-Transaction contains the hashes of source, dest, and amount, and the zk proof is sent to the user, to be redeemed elsewhere. This serves now as an anonymized certified check. The user can now go to another chain, open the dest and the amount values in a private interaction with B Sequencer, show that dest and amount, if hashed, equal the hashed values contained in the proof, and redeem the amount. This allows us to implement privacy guarantees comparable to zcash [4].
Besides Entangled Rollups, there are other interesting applications of a zkVM and other sophisticated variants of rollups imaginable.
Prove zk correctness for one single transaction only Suppose that some transaction is independent of others (it has no side effects), that the transaction is correct (we can prove this using a zkProof), and that the batch has been finalized. Could this lead to shorter prover time for that specific transaction? For instance, one could imagine that the Sequencer cut its computation in slices, where each slice contains exactly one entire transaction. So each transaction will be sandwiched between an initial and final snapshot of the computation, where each snapshot is stored independently. By making these snapshots available on request, the transaction can be verified, either by some other party or by applying a zkProof to the slice only. This may all seem very ambitious, but compared to slicing zkVM proofs, parallelizing them and recombining the proofs of the slices it is nothing. This idea could lead to a differentiated treatment of selected transactions (such as high-value ones).
Identify a subclass of simple and fast transactions We conjecture that a significant percentage of transactions all have the same, simple format, without running a sophisticated smart contract. So for these transactions, correctness verification should be easy (no need to run the full zkVM), and could be optimized for this specific case. We can imagine L2 maintaining two separate transaction queues, leading to two separate batches: one queue (FAST) containing these simple transactions, and another (NORMAL) allowing any format. This could reduce the traditional 7-day withdrawal period associated with OP Rollups to a matter of hours when such transactions gain a zkProof.
Proving asset correctness for L2 Instead of a full-fledged zkProof that the whole batch was processed correctly, we prove in zk that asset correctness is maintained by each and every transaction in the batch. This approach would require much simpler and faster proofs for transactions in the FAST queue, and could be combined with a traditional optimistic rollup. Transactions in the NORMAL queue would continue to be proved with usual zkVM proofs.
Acknowledgement The author is grateful to Lucas Fraga, Stephen Duan, Pavel Sinelnikov and Ming Guo for discussions that helped him to understand this topic and write this paper.